برای دیدن محتوای سایت روی دکمه دسته بندی کلیک بفرمایید

با این مقاله ی آموزنده که شامل تعاریف، مثالها و منابع آموزشی است، معنی تقارن و آنچه که اشکال متقارن را متقارن میکند، خواهید اموخت. وقتی چیزی متقارن است که دو نیمه منطبق داشته باشد. میتوانید تقارن یک شکل را با کشیدن یک خط آینهای در وسط بررسی کنید و ببینید که آیا هر دو نیمه یکسان هستند یا خیر. به عبارت دیگر، تقارن زمانی وجود دارد که چیزی که دارای قطعات منطبق در مقابل یکدیگر یا حول یک محور باشد. اما چه چیزی یک شکل را متقارن می کند؟ به بیان ساده، اشکال متقارن (یا متقارن) یک طرف آن مشابه طرف دیگر هستند. اشکال متقارن پس از بازتاب، چرخش یا ترجمه یکسان به نظر می رسند. اگر بتوانیم خطی را مستقیماً از مرکز یا محور یک شکل بکشیم، به طوری که هر دو طرف خط بازتاب دیگری باشد، در این صورت یک شکل متقارن با تقارن بازتابی است. خطی را که از طریق شکل می کشیم به عنوان خط تقارن نیز یاد می کنیم . یک خط تقارن یک شکل را به دو نیم می کند و دو شکل یکسان از آن ایجاد می کند. هنگام ترسیم این خط، باید وسط دقیق یک شکل یا شکل را پیدا کنید. یک خط تقارن را می توان " خط آینه " نیز نامید زیرا می توان یک آینه در امتداد آن قرار داد و انعکاس کل شکل را نشان می دهد. آینه های کوچک می توانند در کلاس درس مفید باشند تا به کودکان کمک کنند معنای تقارن و نحوه عملکرد آن را درک کنند. چهار نوع تقارن عبارتند از انعکاس چرخشی، انتقالی، بازتابی و لغزشی. که به عنوان تقارن آینه ای یا تقارن خط نیز شناخته می شود ،نوع اصلی تقارن در ریاضیات است که در مدارس تدریس می شود. همچنین به عنوان تقارن شعاعی شناخته می شود . یک شکل یا الگو زمانی تقارن چرخشی دارد که پس از چرخش کمتر از یک دور کامل یکسان به نظر برسد. تقارن دورانی را با تعداد دورهایی که طول می کشد تا یک شکل یکسان به نظر برسد، حساب می کنیم. به این ترتیب تقارن چرخشی می گویند. به عنوان مثال، یک مستطیل دارای مرتبه 2 و یک ستاره پنج نقطه ای دارای ترتیب 5 است. برای نگاهی عمیق به تقارن چرخشی در ریاضیات، به صفحه اختصاصی Twinkl ویکی ما نگاهی بیندازید . تقارن ترجمه ای در ریاضیات کمی پیچیده تر است و باز هم فقط در دبیرستان معرفی می شود. برای اینکه یک شی دارای تقارن انتقالی باشد، باید در جهت معین و در فاصله معینی ترجمه شده باشد، یا شبیه سازی شده و حرکت داده شده باشد. باید بیش از یکی از یک الگو یا شی خاص وجود داشته باشد تا تقارن انتقالی داشته باشد، به همین دلیل است که اغلب مفید است که یک الگوی مکرر را به عنوان نمونه ای از تقارن ترجمه در نظر بگیریم. اگر می خواهید در بالای دیوار خانه خود حاشیه ای از شکل های مربع کوچک داشته باشید، دوست دارید این ها تکرار شوند و در فاصله ای مشابه از یکدیگر باشند. این نمونه ای از تقارن ترجمه ای خواهد بود. تقارن انعکاس لغزشی بهتر است به عنوان ترکیبی بین انعکاس و تقارن انتقالی در نظر گرفته شود. این شامل هر دو فرآیند است، اما در یک نظم خاص. بازتاب روی یک خط، و سپس ترجمه در امتداد خط. یک شکل ابتدا باید منعکس شود و سپس به هر جهتی ترجمه شود تا انعکاس سر خوردن اتفاق بیفتد. احتمالاً دانش آموزان در دوران دبستان با مفهوم تقارن در ریاضیات آشنا می شوند. در اینجا آنها شروع به یادگیری هندسه اشکال دوبعدی ، ویژگیهای هندسی آنها میکنند و دانش پسزمینه مورد نیاز برای شروع درک ویژگیهایی مانند همخوانی و تقارن رابطهای را توسعه میدهند. در سال دوم ، کودکان شروع به یادگیری در مورد تقارن و خطوط تقارن خواهند کرد. در سال چهارم ، کودکان باید خطوط تقارن را در اشکال دوبعدی شناسایی کنند. آنها در مورد خطوط مختلف تقارن در اشکال پی خواهند برد و یاد خواهند گرفت که چگونه خطوط تقارن را در اشکال منظم شناسایی کنند. آنها همچنین ممکن است نیاز به طبقه بندی اشکال با استفاده از ویژگی هایی داشته باشند که شامل خطوط تقارن است. در سال پنجم ، کودکان شروع به یادگیری در مورد بازتاب خواهند کرد. آنها باید از یک خط آینه برای انعکاس اشکال برای تکمیل آنها استفاده کنند. در سال ششم ، کودکان با استفاده از محورها برای انعکاس اشکال، در مورد سطوح هماهنگ و ربع یاد خواهند گرفت. همچنین مشاهده کنید: ویدئوهای آموزش تقارن و قرینه یابی در مام پلاس تقارن از دیدگاه ویکی پدیا : در هندسه ، اگر عملیات یا تبدیلی (مانند ترجمه ، مقیاسبندی ، چرخش یا بازتاب ) وجود داشته باشد که شکل/شیء را بر روی خود نگاشت میکند ، یک شی دارای تقارن است (یعنی شیء دارای یک تغییر ناپذیری در زیر تبدیل است). بنابراین، تقارن را می توان به عنوان مصونیت در برابر تغییر در نظر گرفت. برای مثال، دایرهای که به دور مرکزش میچرخد، شکل و اندازه دایره اصلی را خواهد داشت، زیرا تمام نقاط قبل و بعد از تبدیل قابل تشخیص نیستند. بنابراین گفته می شود که یک دایره تحت چرخش متقارن استیا تقارن چرخشی داشته باشد . اگر ایزومتریک انعکاس یک شکل مسطح در مورد یک خط باشد، به این شکل گفته می شود که دارای تقارن بازتابی یا تقارن خط است . همچنین ممکن است یک شکل/شیء بیش از یک خط تقارن داشته باشد. در ریاضیات، برخی از مفاهیم اساسی، مانند تقارن و بی نهایت، آنقدر فراگیر و قابل انطباق هستند که می توانند برای دانش آموز گریزان شوند. درک این مفاهیم و ابزار مطالعه آنها اغلب یک فرآیند طولانی است که در طول سالیان طولانی در حرفه یک دانش آموز گسترش می یابد. دانشآموزان ابتدا بینهایت را بهعنوان نامتناهی بالقوه ذاتی در سیستم اعداد موقعیتی میبینند، سپس به صورت ضمنی در هندسه صفحه، و در نهایت زیربنای تمام محاسبات و تجزیه و تحلیل. دانش آموزان شروع به استفاده از تقارن با جابجایی و تداعی در حساب می کنند و از آن در هندسه اقلیدسی و هندسه صفحه استفاده بیشتری می کنند و در نهایت ممکن است آن را بر حسب گروه های تبدیل ببینند. با این وجود، طبیعی است که بخواهیم این مفاهیم را از همان ابتدا با ارزش کامل آموزش دهیم. تقارن در همه جای طبیعت یافت می شود و همچنین یکی از رایج ترین موضوعات در هنر، معماری و طراحی است .تقارن مطمئناً یکی از قدرتمندترین و فراگیرترین مفاهیم در ریاضیات است. در عناصر، اقلیدس از همان گزاره اول از تقارن بهره برد تا برهان های خود را روشن و صریح کند. گالوا با تشخیص تقارنی که در بین ریشه های یک معادله وجود دارد، توانست مسئله ای چند صد ساله را حل کند. ابزاری که او برای درک تقارن ایجاد کرد، یعنی نظریه گروه، از آن زمان توسط ریاضیدانان برای تعریف، مطالعه و حتی ایجاد تقارن استفاده شده است. دانش آموزان مجذوب نمونه های عینی تقارن در طبیعت و هنر هستند. مطالعه قرینه یابی می تواند به همان اندازه ابتدایی یا پیشرفته باشد که فرد بخواهد. برای مثال، میتوان به سادگی تقارن طرحها و الگوها را پیدا کرد، یا از گروههای تقارن بهعنوان روشی قابل درک برای آشنا کردن دانشآموزان با رویکرد انتزاعی ریاضیات مدرن استفاده کرد. علاوه بر این، ایدههایی که ریاضیدانان در مطالعه قرینه یابی به کار میبرند، منحصر به ریاضیات نیست و میتوان آن را در حوزههای دیگر تفکر بشری نیز یافت. با نگاه کردن به تقارن در یک زمینه گسترده تر، دانش آموزان می توانند ارتباط ریاضیات را با سایر شاخه های دانش ببینند. به این دلایل، امروزه بسیاری از ریاضیدانان احساس می کنند که مطالعه ریاضی تقارن برای دانش آموزان آموزش عمومی ارزشمند است. ایده اصلی در مطالعه ریاضی تقارن، تبدیل تقارن است که میتوانیم آن را به عنوان یک همشکلی که دارای برخی متغیرها است ببینیم. برای مثال، تبدیل تقارن یک طرح در صفحه، ایزومتری است که مجموعه خاصی از نقاط را به عنوان یک مجموعه ثابت میگذارد. من میخواهم دانشآموزان بدانند که این مفهوم از تبدیل تقارن، هر چند انتزاعی به نظر میرسد، میتواند به ایدههایی مرتبط باشد که ممکن است برای دیدگاهی از زندگی به عنوان یک کل محوریتر به نظر برسند. یک شکل هندسی که ما می خواهیم مطالعه کنیم معمولاً به عنوان مجموعه ای از نقاط موجود در برخی از فضای محیط ارائه می شود. به عنوان مثال، یک الگوی کاشی کاری ممکن است به عنوان مجموعه ای از قطعات خط در صفحه ارائه شود. تبدیل تقارن را می توان به عنوان "عمل" در نظر گرفت و متغیرها را می توان به عنوان "انفعال" در نظر گرفت. ما با یک وضعیت غیر پویا (مجموعه نقاط الگوی کاشی کاری نشسته در صفحه) شروع می کنیم و سپس مقداری پویایی (تحول تقارن) پیدا می کنیم. بنابراین، در انفعال، عمل را می بینیم. اما تبدیل تقارن فقط هر عملی نیست. باید الگوی (به عنوان مجموعه ای از نقاط) را ثابت بگذارد. بنابراین، آنچه برای ما مهم است این است که در این عمل (تحول)، ما قادر به مشاهده عدم عمل (عدم تغییر مجموعه ای از نقاط تشکیل دهنده الگو) هستیم. این اصل همه چیزهایی است که من میخواهم دانشآموزان درباره تقارن بدانند: کنش و عدم کنش، یک دگرگونی و متغیرهای آن، چه چیزی تغییر میکند و چه چیزی ثابت میماند. با این کار، دانشآموزان دیدگاه واحدی در مورد مفهوم تقارن به دست میآورند که میتواند به آنها در درک اولیه آن کمک کند و بعداً میتواند به آنها کمک کند تا تمام رخدادهای این مفهوم را هنگام ملاقات ساده و یکسان کرده و در نهایت گروههای تقارن، متغیرها و غیره را درک کنند. بر. این موضوع همچنین میتواند به دانشآموزان کمک کند تا تمام نمونههای تقارن را که قبلاً دیدهاند، به این دیدگاه وحدتبخش مرتبط کنند. مثلاً در خصوصیات جابجایی و تداعی حساب، موقعیت اعداد یا پرانتزها تغییر می کند، اما پاسخ تغییر نمی کند. برای کاشی کاری، صفحه اقلیدسی را می توان به روش های خاصی چرخاند، منعکس کرد یا ترجمه کرد، اما الگوی یکسان باقی می ماند. دانش آموزان با ایده های نسبتاً محدودی از تقارن به ریاضیات می آیند. اغلب کلمه تقارن به معنای "تقارن دو طرفه" تفسیر می شود و نه چیزی بیشتر. با این وجود، آنها قبلاً تقارن را به اشکال مختلف دیدهاند: طبیعت، اشیاء ساخته شده، هنر و معماری، و حتی در ریاضیات (جابهجایی، دایرهها و مربعها، توابع زوج و فرد، و غیره). برای دانش آموزان خوب است که درک درستی از تقارن داشته باشند که شامل تمام مثال هایی است که دیده اند و پایه ای برای مطالعه بیشتر می گذارد. من می خواهم آنها را با ایده تبدیل تقارن آشنا کنم، حتی اگر آنها ندانند یک تابع چیست، تا آن را به خاطر بسپارند، احساس کنند مهم است و بتوانند از آن استفاده کنند. دانشآموزان باید بدانند که تقارن برخی از ویژگیهای زیرین را مشخص میکند که ممکن است انتزاعیتر و کمتر آشکار باشد، اما یکپارچهتر و متمایزتر است. همچنین میخواهم دانشآموزان بینشی در مورد اینکه چرا تقارن برای ما جذاب است و از نظر زیباییشناختی جذاب است، داشته باشند. هنگامی که دانش آموزان شروع به طراحی الگوهای خود می کنند، شروع به فکر کردن از نظر زیبایی شناسی می کنند، اینکه چه الگوهایی را دوست دارند و می خواهند روی خودشان کار کنند. تقارن زیبا و جذاب است. از جذابیت یک دانه برف تا معنویت عمیق شام آخر لئوناردو، تقارن نقش اساسی در طبیعت و هنر دارد. آیا درک تقارن که در اینجا به دست آورده ایم می تواند به ما در درک این نقش کمک کند؟ دیدهایم که یک الگوی متقارن باعث ایجاد تقارن یا دگرگونیهای الگو میشود که اساساً آن را بدون تغییر میگذارد. از باگاواد-گیتا می بینیم که زندگی دو جنبه دارد، فعال و غیر فعال. به عقیده ماهاریشی [م]، سطح خاموش زندگی، آگاهی ناب، منبع اندیشه است و به طور ذهنی به عنوان سعادت تجربه می شود. هر گاه سطح فعال ذهن شروع به حرکت در جهت سطح خاموش ذهن کند، سعادت فزاینده ای وجود دارد. یک الگوی هنری یا ساختار طبیعت بیانگر تنوع وجود نسبی است، با این حال، در تکرار جنبه های طرح یا ساختار، یعنی در تقارن، یک همسانی یا مقدار یکسان کننده زیرین نشان داده می شود. ذهن به طور خود به خود به تجربه فعالیت و سکوت به طور همزمان سوق داده می شود. این در جهت ماهیت تجربه ای است که در آیه بهاگاواد گیتا که بررسی کردیم شرح داده شده است. بنابراین، تجزیه و تحلیل ما می تواند به روشن کردن ماهیت جذاب تقارن کمک کند. ریاضیات بخشی از زندگی است. ریاضیدانانی که ریاضیات را انجام می دهند، تابع قوانین طبیعی یکسانی هستند که بر تمام زندگی حاکم است. درک عمیق از کل زندگی باید به ما بینشی بدهد که به ما در درک بخشهای زندگی، از جمله جنبههای بسیار خاص ریاضیات کمک کند. این مقاله نشان میدهد که چگونه میتوان از یک بیان دانش در مورد ماهیت زندگی برای ورود عمیق به مطالعه ریاضی تقارن استفاده کرد و امیدواریم به عنوان پیشنهادی عمل کند که این ترکیب ریاضیات و زندگی به عنوان یک کل میتواند به روش های دیگر انجام شود. تقارن در ریاضیات
معنی تقارن در ریاضیات
معنی خطوط تقارن :
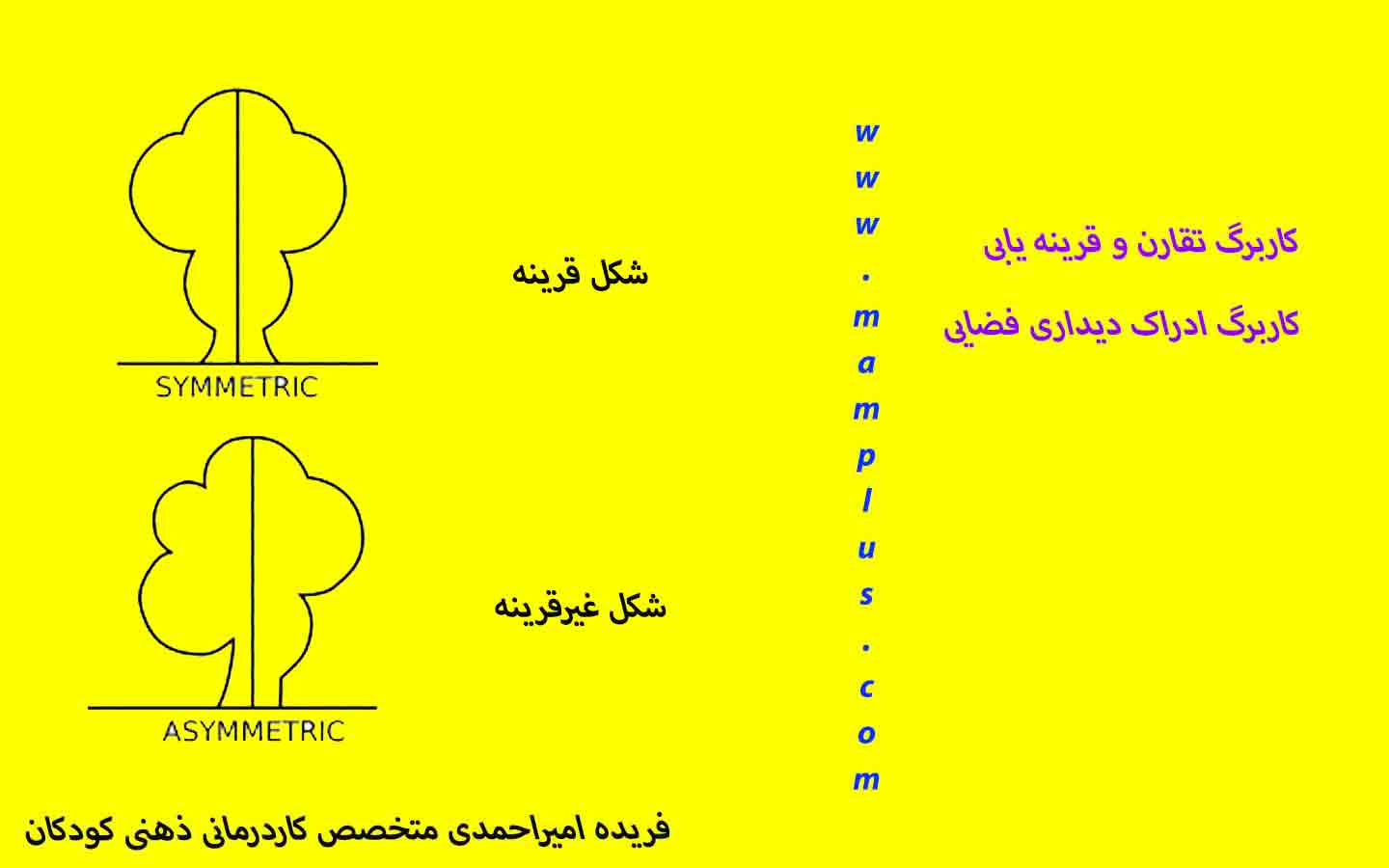
چهار نوع تقارن چیست؟
1.تقارن بازتابی
2.تقارن چرخشی
3.تقارن ترجمه ای
4.تقارن بازتاب سر خوردن
تقارن از چه زمانی در مدارس مطرح می شود؟
چه زمانی کودکان در دبستان تقارن را یاد می گیرند؟
نگاه فلسفی به قرینه یابی و ارتباط آن با ریاضیات :
تقارن یا اکمال بینایی چیست ؟
چرا تقارن را آموزش دهیم؟

پیوندی بین تقارن و زندگی
آموزش تقارن
زیبایی تقارن
نتیجه :